The purpose of this article is to provide an overview of different properties of fluids and its classification. It aims to educate readers on the fundamental concepts of fluids, including their definition and how they differ from solids and gases. The article also covers different types of fluids based on flow characteristics, such as steady or unsteady, compressible or incompressible, viscous or non-viscous, and rotational or irrotational.
Furthermore, the article explores various properties exhibited by fluids, including density, viscosity, temperature, pressure, specific volume, specific weight, specific gravity, surface tension, vapor pressure, capillarity, and cavitation. By understanding these properties, readers can gain insights into how fluids behave and interact with their surroundings. The article aims to be comprehensive, covering all the mentioned topics in detail.
Table of Contents

What is Fluid?
Fluid is a state of matter that is characterized by its ability to flow and conform to the shape of its container. Unlike solids, which have a definite shape and volume, and gases, which have neither a definite shape nor volume, fluids are capable of flowing and taking on the shape of the container in which they are placed. This ability to flow is due to the relatively weak intermolecular forces and high mobility of the particles or molecules within fluids.
Fluids can be differentiated from solids and gases based on their flow properties and characteristics. Here are the key differences:
1. Shape:
Solids have a definite shape and maintain their shape even when subjected to external forces. Gases, on the other hand, have no fixed shape and expand to fill the entire available space. Fluids, including both liquids and gases, can change their shape and conform to the shape of the container they occupy.
2. Volume:
Solids have a fixed volume and retain their shape, whereas gases have no fixed volume and can expand or compress to occupy the available space. Fluids, however, can have a variable volume depending on the external conditions and the constraints of the container.
3. Particle Arrangement:
In solids, particles are closely packed together in a regular and ordered arrangement, forming a rigid structure. In gases, particles are widely spaced and move randomly, colliding with each other and the container walls. Fluids have particles that are more loosely packed compared to solids but closer together compared to gases. The arrangement of fluid particles can be more random or organized, depending on the type of fluid.
4. Intermolecular Forces:
Solids have strong intermolecular forces that hold their particles tightly together, while gases have weak intermolecular forces. Fluids possess intermediate intermolecular forces, allowing their particles to move and flow but still exhibit some level of cohesion.
5. Rigidity:
Solids are rigid and resist deformation under applied forces, whereas gases readily undergo large deformations. Fluids are less rigid compared to solids but more resistant to deformations compared to gases.
6. Shear Stress:
Solids do not readily flow under the influence of shear stress and require significant force to cause deformation. Gases flow easily under shear stress. Fluids, by definition, flow under the influence of shear stress and can readily deform when subjected to external forces.
Fluids can be distinguished from solids and gases based on their ability to flow, change shape, and conform to the shape of their container. While solids have a definite shape and volume, and gases have neither a definite shape nor volume, fluids possess the unique characteristic of flow, making them distinct from the other states of matter.
TYPES OF FLUIDS
The categorization of fluids based on their flow characteristics includes the following types:
1. Steady or Unsteady Flow:
Steady Flow:
In steady flow, the fluid’s velocity at any given point does not change with time. The flow characteristics, such as velocity, pressure, and cross-sectional area, remain constant over time. The flow pattern does not change. Example: Water flowing steadily through a pipe without any changes in velocity or flow rate.
Unsteady Flow:
Unsteady flow refers to a condition where the fluid’s velocity varies with time. The flow characteristics change over time due to variations in velocity, pressure, and cross-sectional area. The flow pattern may change over time. Example: Waves in the ocean, where the water velocity and surface conditions vary with time.
2. Compressible or Incompressible Flow:
Compressible Flow:
Compressible flow occurs when the density of the fluid changes significantly under the influence of pressure variations. These fluids can be compressed or expanded, and changes in pressure affect their density. Example: Air flowing through a jet engine during supersonic flight, where changes in pressure significantly affect the density of the air.
Incompressible Flow:
In incompressible flow, the fluid’s density remains nearly constant regardless of changes in pressure. The density variations are negligible, and the fluid cannot be significantly compressed or expanded. Liquids are often considered incompressible for most practical applications. Example: Water flowing through a hydraulic system, where the density remains nearly constant despite changes in pressure.
3. Viscous or Non-viscous Flow:
Viscous Flow:
Viscous flow refers to the flow of a fluid that exhibits internal resistance to flow or shear. These fluids have a certain level of stickiness or resistance to deformation. The rate of deformation is directly proportional to the applied shear stress. Example: Honey flowing down a spoon, where the resistance to flow is noticeable due to the high viscosity of honey.
Non-viscous Flow:
Non-viscous flow describes the flow of a fluid with negligible internal resistance to flow. These fluids have very low or no viscosity and flow easily without any significant resistance to deformation. Example: Ideal gas flowing through a pipeline, where the gas molecules have low intermolecular forces and flow easily without significant resistance.
4. Rotational or Irrotational Flow:
Rotational Flow:
Rotational flow occurs when fluid particles move in a rotational or circular pattern around an axis. The particles have both translational and rotational motion, creating swirling or vortex-like patterns. This type of flow is present in tornadoes, whirlpools, and many fluid mixing processes. Example: Water swirling around in a whirlpool, where the fluid particles move in a circular pattern with rotational motion.
Irrotational Flow:
Irrotational flow refers to the flow of fluid particles without any rotation. The fluid particles move only with translational motion, and there are no swirling or vortex patterns present in the flow. Example: Water flowing smoothly over a streamlined object, such as an airplane wing, where the fluid particles move without any rotational motion.
These different types of fluid flow provide a basis for categorizing and analyzing fluid behavior in various situations. Understanding the nature of flow helps in studying and predicting fluid dynamics and is essential in many engineering and scientific applications.
You can also practice STUDY CENTRIFUGAL PUMP- PERFORMANCE CHARACTERISTICS TEST.
Properties of Fluids
Fluids exhibit various properties that are essential for understanding their behavior and analyzing their interactions with their surroundings:
1. Density:
Density is the mass per unit volume of a fluid. In the case of gases, the density is dependent on both pressure and temperature, as changes in these parameters can significantly affect the gas molecules’ behavior. On the other hand, the density of liquids remains relatively constant, with minimal variations under normal conditions. The density of water is approximately 1000 kg/m^3, meaning that one cubic meter of water weighs 1000 kilograms. This value serves as a reference point for comparing the densities of other substances.
ρ=mass/volume
2. Viscosity:
Viscosity is a measure of a fluid’s resistance to flow or its internal friction. It represents the tendency of a fluid to resist its movement over a surface. In fluids, viscosity arises due to cohesive forces between molecules, while in gases, it is attributed to molecular momentum transfer. A fluid with high viscosity experiences greater internal friction, leading to increased resistance to flow.
F=μA(u/y)
If the velocity of a fluid does not vary with the y-direction, it can be expressed using the following relationship:
τ=μ(∂u/∂y)
Kinematic viscosity, denoted by ν, is a term commonly used in fluid dynamics to describe the viscosity of a fluid. It is defined as the ratio of the dynamic viscosity (μ) to the density of the fluid (ρ).
ʋ = μ/ρ
SI unit=m^2/s; Dimensional formula = [M^0L^2T^(-1)][M^0L^2T^(-1)]
Effects of temperature and pressure on μ & ʋ
In liquid; T↑-μ↓-ʋ↓, In gases; T↑-μ↑-ʋ↑
Dynamic viscosity, denoted by μ, is a measure of the absolute viscosity of a fluid. It is obtained by dividing the shear stress experienced by the fluid by the rate of shear strain. SI unit=Pa·s
Units of dynamic viscosity : Force / area x time
3. Temperature:
Temperature represents the average kinetic energy of the particles within a fluid. It determines the thermal state of the fluid and influences its density, viscosity, and other properties. Temperature is typically measured in degrees Celsius (°C) or Kelvin (K).
4. Pressure:
Pressure is the force per unit area exerted by a fluid on its surroundings. It arises from the collision of fluid molecules with the walls of a container or surfaces immersed in the fluid. Pressure is an essential property in fluid mechanics and is often measured in units such as pascal (Pa), atmosphere (atm), or pounds per square inch (Psi).
Pressure of the fluid = Force/Area
5. Specific Volume:
Specific volume is the reciprocal of density and represents the volume occupied by a unit mass of fluid. It is a measure of how much space a given mass of fluid occupies. Specific volume is denoted by the symbol v and is typically measured in cubic meters per kilogram (m³/kg).
S = 1/ρ = volume/mass
6. Specific Weight:
Specific weight is the weight per unit volume of a fluid. It is the product of the density and the acceleration due to gravity (g). Specific weight is denoted by the symbol γ or W and is commonly measured in units of newtons per cubic meter (N/m³) or pounds per cubic foot (lb/ft³).
W = weight/volume
Since, weight w=mg
Density ρ=m/v
So, W= mg/v
Therefore, the specific weight can be expressed as W = ρg
The dimensional formula of specific weight is [M1L−2T−2][M1L−2T−2]
7. Specific Gravity:
Specific gravity denoted by S is the ratio of the density of a fluid to the density of a reference substance, usually water at a specified temperature. It provides a measure of a fluid’s relative density compared to water. Specific gravity is a dimensionless quantity.
S=Density of Fluid/Density of the standard Fluids
Specific volume is a unitless and dimensionless quantity that provides information about how much space a unit mass of a substance occupies.
Specific volume, denoted by V, is defined as the volume per unit mass of a substance, typically a liquid. It can be calculated by dividing the volume (V) of the substance by its mass (m). Alternatively, it can be expressed as the reciprocal of density (ρ), where ρ is the density of the substance.
V=v/m or 1/ρ
Specific Gravity for liquid = ρ(liquid)/ρ(water)
Specific Gravity for gas = ρ(gas)/ρ(air)
Weight of fluid = ρ.g.v
Note: SG>1; heavier than water, SG<1; lighter than water
Numerical data: SG=13.6 (Hg), SG=1(water)
8. Surface Tension:
Surface tension is the property of a fluid that describes the cohesive forces between its molecules at the liquid-gas interface. It causes the surface of a liquid to behave like a stretched elastic sheet, minimizing the surface area. Surface tension influences phenomena such as capillary action and the formation of droplets. It is denoted by 𝝈 and has an SI unit of Newton per meter. The dimensional formula of surface tension is [M1L1T-2]
𝝈 = F/L
𝝈 =(1/2)( F/L); The reason for the factor of 1/2 is that a liquid film has two surfaces, and each contributes equally to the force.
Surface tension can also be expressed as the work done divided by the change in surface area, where work is the change in energy of the liquid and ΔA is the change in surface area.
𝝈=F/2L = FΔx/2LΔx=W/ΔA
W= work done; F= force applied on surface; ΔA=change in surface area; 𝝈=surface tension at room temperature
Increase in forces of pressure = force due to surface tension
Water droplet or bubble inside water=4𝝈/d
Soap bubble=8𝝈/d
water jet=2𝝈/d
9. Vapor Pressure:
Vapor pressure is the pressure exerted by the vapor phase of a substance when it is in equilibrium with its liquid or solid phase at a specific temperature. It represents the tendency of a substance to evaporate and is affected by temperature and the intermolecular forces within the substance.
T↑-Pv↑; more volatality↑-Pv↑
10. Capillarity:
Capillarity is the phenomenon by which fluids rise or are drawn into narrow tubes or capillaries due to adhesive and cohesive forces. It is influenced by the interplay of surface tension, adhesion to the capillary walls, and the wetting properties of the fluid.
The height to which a liquid rises in a capillary tube can be calculated using the capillary action formula:
h = (2γ * cosθ) / (ρ * g * r)
Where:
h= Height of the capillary tube.
r = Radius of the capillary tube.
θ = Contact angle between the liquid and the tube’s surface.
ρ = Density of the liquid.
γ = Surface tension at room temperature.
g = Acceleration due to gravity.
For a water-filled glass tube in air at standard laboratory conditions, with γ = 0.0728 N/m at 20 °C, ρ = 1000 kg/m3, and g = 9.81 m/s2, the approximate height of the water column can be expressed as:
h ≈ 1.48 × 10^(-5) * r
This equation gives an estimation of the height based on the radius of the capillary tube.
11. Cavitation:
Cavitation occurs when the pressure of a fluid drops below its vapor pressure, resulting in the formation and subsequent collapse of vapor bubbles. It can cause damage to surface and components and is often undesirable in fluid systems.
Pmin > Pvs = Normal flow = Designing condition
Pmin < Pvs = Boiling will start = Bubbles are formed
12. Wetting and Non-wetting Phenomenon:
A wetting liquid is a liquid that forms a contact angle with a solid surface smaller than 90 degrees. In this case, the adhesive force between the liquid and the solid is more effective than the cohesive force within the liquid itself. On the other hand, a non-wetting liquid creates a contact angle between 90 degrees and 180 degrees with the solid surface. In this case, the cohesive force within the liquid is more prominent than the adhesive force between the liquid and the solid.
These properties play crucial roles in understanding and analyzing fluid behavior, as well as in engineering and scientific applications involving fluid mechanics, thermodynamics, and transport phenomena.
Types of Fluids
There are several types of fluids, each with distinct characteristics. Here is a brief overview of some common types:
1. Ideal Fluid:
An ideal fluid is a theoretical concept used in fluid dynamics to simplify calculations and analysis. It represents a fluid that is frictionless, incompressible, and non-viscous. In an ideal fluid, there is no internal friction or resistance to shear, meaning it flows smoothly without any energy loss. It does not experience changes in density or volume when subjected to external forces or pressure variations.
Ideal fluids follow mathematical equations that allow for straightforward calculations and predictions of fluid behavior. While ideal fluids do not exist in reality, they serve as a useful reference for understanding fluid dynamics and as a basis for comparison with real fluids.
An ideal fluid is assumed to be inviscid, meaning it has no internal friction or viscosity. Inviscid fluids do not experience resistance to shear or flow, allowing them to move without any energy losses due to friction.
µ = 0
Ideal fluids are considered to have cohesive forces between their molecules, which gives rise to surface tension. Surface tension is the property that causes the surface of a liquid to behave like a stretched elastic sheet, minimizing its surface area. Ideal fluids exhibit perfect surface tension, resulting in smooth, uniform surfaces.
Cohesive Forces = 0, Surface Tension = 0
Ideal fluids are often assumed to be incompressible, meaning their density remains constant regardless of external pressure changes. In practical terms, this assumption holds for most liquids under normal conditions, while gases are considered compressible fluids due to their significant density changes with pressure variations.
ρ = c; c=constant
While ideal fluids are typically assumed to be incompressible, certain fluid flow situations may require considering compressible fluids. Compressible fluids, such as gases, experience changes in density and volume when subjected to variations in pressure and temperature.
ρ ≠ c; c=constant
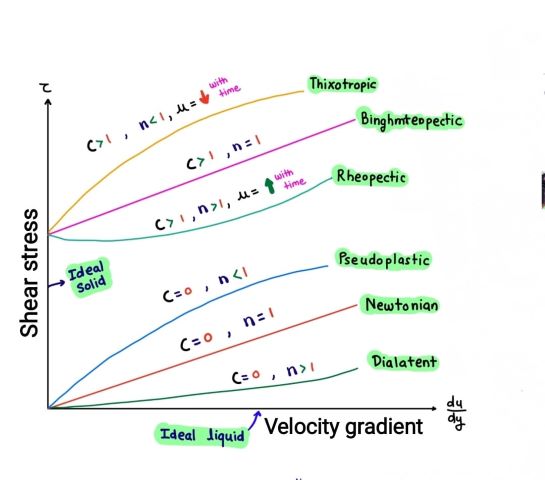
| Type of Fluid | Example |
| Thixotropic | Ice-cream |
| Binghm Plastic | Toothpaste, Gel |
| Rheopectic | Printer ink, Gypsum in water |
| Pseudoplastic | Blood, Milk, Lipstick, Paint |
| Newtonian | Water, Air |
| Dilatant | Quick Sand, Starch, Sugar soln. |
2. Real Fluid:
A real fluid refers to an actual fluid found in nature or encountered in practical applications, in contrast to the idealized concept of an ideal fluid. Unlike ideal fluids, real fluids exhibit properties such as viscosity, compressibility, and thermal expansion. These properties make real fluids more complex and diverse in their behavior compared to the simplified assumptions of ideal fluids. Real fluids follow the laws of fluid mechanics and can vary in viscosity, which is a measure of their resistance to flow.
3. Newtonian Fluid:
A Newtonian fluid is a type of real fluid that follows Newton’s law of viscosity. According to this law, the rate of shear stress is directly proportional to the rate of shear strain. In other words, the viscosity of a Newtonian fluid remains constant regardless of the applied shear rate. Examples of Newtonian fluids include water, air, and most common liquids. These fluids have a consistent and predictable flow behavior, making them relatively straightforward to analyze in terms of fluid mechanics. Newtonian fluids are characterized by their ability to flow smoothly and exhibit a linear relationship between shear stress and shear rate.
τ = η × i (shear stress=viscosity ×shear strain rate)
This relationship can be expressed as; τ = η × (du/dy)
where τ is the shear stress, η is the dynamic viscosity, and du/dy is the velocity gradient.
4. Non-Newtonian Fluid:
A non-Newtonian fluid is a type of fluid that does not follow Newton’s law of viscosity. Unlike Newtonian fluids, the viscosity of non-Newtonian fluids can vary with the shear rate, shear stress, or other external factors. This means that their flow behavior is more complex and can exhibit characteristics such as shear-thinning (decreasing viscosity with increasing shear rate) or shear-thickening (increasing viscosity with increasing shear rate). Non-Newtonian fluids can be found in various forms, such as gels, slurries, or emulsions. Examples include ketchup, toothpaste, and blood.
τ=constant×(dy/dx)^n
5. Ideal Plastic Fluid:
An ideal plastic fluid is a type of non-Newtonian fluid that exhibits properties of both solids and fluids. It behaves like a solid until a certain yield stress is exceeded, at which point it starts flowing like a viscous fluid. Ideal plastic fluids are characterized by their ability to withstand and transmit stresses up to a certain point before transitioning into a flowing state. This yield stress is a critical parameter that determines the behavior of the fluid. Below the yield stress, the ideal plastic fluid retains its shape and acts as a solid, while above the yield stress, it deforms and flows like a fluid. Ideal plastic fluids are often used to model materials such as clay or other viscoelastic substances that exhibit a combination of solid and fluid behavior.
6. Incompressible Fluid:
An incompressible fluid is a fluid whose density does not significantly change with variations in pressure. Expansion and contraction of an incompressible fluid can occur under diabatic heating or cooling, where the temperature changes. However, in the more common scenario of isothermal processes, where the temperature remains constant, the fluid does not change its density when moving between regions of higher or lower pressure. Mathematically, this means that while the density gradient (∇ρ) and the local derivative (∂ρ/∂t) may not be zero, the individual derivative representing the change in density of a fluid parcel as it moves (Dρ/Dt) is zero. This condition is derived from the equation of continuity, which relates the divergence of fluid velocity (u, v, w) to the density changes.
∇.u = (∂u/∂x)+(∂v/∂y)+(∂w/∂z) = 0
7. Compressible Fluid:
A compressible fluid is a fluid that experiences changes in density with variations in pressure and temperature. Gases, such as air and other gases used in engineering applications, are compressible fluids. Compressible fluid dynamics involve studying the behavior of fluids under high-pressure conditions, such as in aerodynamics and gas dynamics.
When the pressure on a given mass of fluid increases (Δp > 0), the volume of the fluid decreases (ΔV < 0)
Denoted by β, is a quantity that represents the compressibility of a substance. It is measured in units of Pa^(-1) and its dimensional formula is [M^(-1)L^(1)T^(2)][M^(-1)L^(1)T^(2)].
β=1/K OR β=(−1/V).(dV/dP)
K = Bulk modulous of elasticity or coefficient of compressibility
For ideal gas:
PV=Constant for Isothermal Process, (PV)^ϒ = Constant for Adiabatic Process
For Hg=β↑, Hg responds very well to ΔT(change in temp.) = used in thermometers
T↑-P↑-K↑-β↓
These are some of the main types of fluids encountered in the study of fluid mechanics and practical applications. Understanding their characteristics is crucial for analyzing fluid flow, designing systems, and predicting fluid behavior in various fields of science and engineering.
Acknowledgement-Fluid Article WIKIPEDIA


